Als aktuell sicherstes Verschlüsselungsverfahren gilt nach CHIP online die so genannte RSA-Methode, ein asymmetrisches Verschlüsselungsverfahren, welches auch beispielsweise in der populären Verschlüsselungssoftware „Pretty Good Privacy“ (PGP) eingesetzt wird. Doch was zeichnet diesen Verschlüsselungs-Algorithmus aus, der - aufgrund seiner Zuverlässigkeit - zudem im Rahmen von e-Banking und e-Voting herangezogen wird? Der folgende Beitrag versucht dieser Frage auf den Grund zu gehen.

=> RSA-Verschlüsselung

In Anbetracht einer Seminararbeit, welche ich in diesem Semester zum Thema e-Voting verfassen werde, möchte ich die Gelegenheit nutzen, in meinem Weblog das RSA-Verschlüsselungsverfahren vorzustellen, welches bereits im Zuge des elektronischen Wählens (beispielsweise bei den estnischen Kommunalwahlen im Oktober diesen Jahres) zum Einsatz kommt. Der Rivest-Shamir-Adleman (kurz RSA) Algorithmus gilt als das derzeit „bewährteste und am besten untersuchte asymmetrische Verschlüsselungsverfahren.“ (Cisco Systems) In den Jahren 1977/78 von Ron Rivest, Adi Shamir und Len Adleman am Massachusetts Institute of Technology (MIT) entwickelt, kommt diese Verschlüsselungsmethode mittlerweile – aufgrund ihrer Sicherheit - in unterschiedlichsten Bereichen zum Einsatz (vgl. Mekelburg 2004). So setzen etwa Banken im Rahmen des e-Banking, Pay-TV-Sender bei der Verschlüsselung ihrer Programme oder aber auch Geheimdienste auf die Vorzüge von RSA. Ferner verwendet die Verschlüsselungs-Software PGP – Pretty Good Privacy, welche auch in der Vorlesung zur Ansprache kam, die RSA-Variante (vgl. Grupp 2001).

Doch wie funktioniert nun der angesprochene RSA-Verschlüsselungs-Algorithmus? Hierzu möchte ich nicht zu sehr ins Detail gehen, da die einzelnen Verschlüsselungsschritte für Nicht-Informatiker bzw. Mathematiker wohl kaum nachvollziehbar wären. Da das RSA-Verfahren zu den so genannten asymmetrischen Verschlüsselungsmethoden zählt, möchte ich mit einem populären Darstellungsbeispiel beginnen, welches die Problematik des symmetrischen Verschlüsselungsverfahrens sehr gut zu veranschaulichen vermag:

„Man stelle sich vor, Alice möchte Bob eine geheime Nachricht senden. Diese legt Alice in eine Kiste, die sie mit einem Schloss sichert und an Bob schickt. Wenn Bob die Kiste erhält, kann er sie nicht öffnen, da er nicht den richtigen Schlüssel besitzt. Alice könnte den richtigen Schlüssel in eine zweite Kiste legen und diese wiederum an Bob schicken; und so weiter und so fort. Bob kann aber auch die zweite Kiste nicht ohne den passenden Schlüssel öffnen. Die einzige Möglichkeit scheint darin zu bestehen, dass sich Alice und Bob treffen und Alice Bob eine Kopie des Schlüssels übergibt. In die Terminologie der Kryptographie übersetzt bedeutet dies, dass Bob die von Alice verschlüsselte Nachricht nur entschlüsseln kann, wenn er von Alice eine Kopie des Schlüssels erhält.

Eine andere Ansatzmöglichkeit besteht darin, dass Bob die verschlossene Kiste mit der Nachricht seinerseits mit einem Schloss sichert und sie an Alice zurückschickt. Alice entfernt daraufhin ihr Schloss und schickt die nur noch mit Bobs Schloss gesicherte Kiste an Bob zurück, der sie mühelos mit seinem Schlüssel öffnen kann.“ (Emmel)



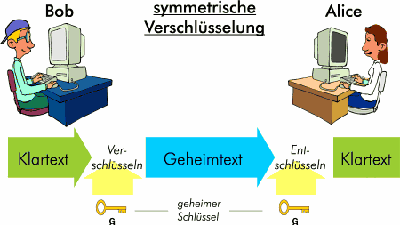
Wie dadurch bereits schön verdeutlicht wird, müssen beim symmetrischen Verfahren Sender und Empfänger einer verschlüsselten Nachricht den Schlüssel, mit welchem der Algorithmus ausgeführt wurde, jeweils untereinander austauschen (vgl. Emmel). Ein Nachteil, welcher in der asymmetrischen Variante durch die Verwendung eines Schlüsselpaares umgangen wird. So besteht zwischen dem Schlüssel der Chiffrierung und jenem zur Dechiffrierung kein Zusammenhang, weshalb auch durch das Wissen des einen Schlüssels nicht auf den jeweils anderen geschlossen werden kann (vgl. Mekelburg 2004). Der Dechiffrierschlüssel muss geheim gehalten werden, der Chiffrierschlüssel zur Verschlüsselung ist jedoch öffentlich zugängig (vgl. Emmel).

„Wenn Bob Alice eine Nachricht schicken will, chiffriert er sie mit Alices öffentlichem Schlüssel. Nur Alice, die ihren geheimen Dechiffrierschlüssel kennt, kann die Nachricht dechiffrieren.“ (Emmel)



Der Vorteil asymmetrischer Verfahren liegt auf der Hand: Es muss kein sicherer Kanal für den Austausch der Schlüssel existieren, wodurch die Übermittlung öffentlich stattfinden kann. Außerdem wird für die Kommunikation eine geringere Anzahl von keys benötigt, da bei der symmetrischen Verschlüsselung für jedes Kommunikationspaar ein Schlüssel erforderlich ist (vgl. Mekelburg 2004). Die Sicherheit von RSA basiert nun in weiterer Folge auf dem Umstand, eine große ganze Zahl in ihre Primfaktoren zu zerlegen. Die beiden Schlüssel werden wie folgt erzeugt, abermals am Beispiel von Bob und Alice:

1. Zunächst muss Alice zwei sehr große Primzahlen p und q auswählen und sie geheim halten. Beispielsweise könnte sie der Einfachheit halber p = 17 und q = 11 wählen.

2. Im zweiten Schritt multipliziert Alice p und q miteinander und berechnet damit die Zahl N. Im Beispiel ist N gleich 187. Nachdem N berechnet ist, muss Alice wiederum eine Zahl e auswählen; sie wählt beispielsweise e = 7. Die Zahlen e und (p – 1)(q – 1) sollten dabei teilerfremd sein.

3. Alice hat mit der Berechnung von N und der Wahl von e ihren öffentlichen Schlüssel erstellt. Sie kann nun beide in einem öffentlichen Verzeichnis hinterlegen, da beide Zahlen für die Verschlüsselung notwendig sind. Die Zahl e kann dabei bei mehreren Personen gleich sein, jedoch muss sich der Wert von N für alle unterscheiden.

4. Eine Mitteilung kann nur verschlüsselt werden, wenn sie in eine Zahl M umgewandelt wurde. Dies kann beispielsweise durch die Interpretation der ASCII-Darstellung als Dezimalzahl geschehen. M kann nach der Formel C = M e(mod N) verschlüsselt werden, wobei C der Geheimtext ist.

5. Wenn Bob Alice den Buchstaben X, der in ASCII durch den Wert 1011000 dargestellt wird, schicken möchte, wandelte er sie in eine Dezimalzahl um. 1011000 entspricht der Zahl 88 im Dezimalsystem, womit gilt: M = 88.

6. Zunächst muss Bob sich Alices öffentlichen Schlüssel beschaffen mit N = 187 und e = 7, die er in die Verschlüsselungsformel einsetzen kann. Damit ergibt sich für C: 88 7(mod 187) = 11(mod 187) und somit C = 11. Bob kann jetzt C an Alice verschicken.

7. Alice berechnet mit ihren geheimen Werten p und q die Zahl d nach der Formel e . d = 1(mod (p - 1)(q - 1)). Sie berechnet 7 . d = 1(mod 16 . 10) beispielsweise mit dem euklidischen Algorithmus und erhält für d den Wert 23.

8. Mithilfe von d kann Alice die Nachricht entschlüsseln, indem sie M = C d(mod N) rechnet., also M = 11 23(mod 187) = 88. (Emmel)

Die Sicherheit des RSA-Algorithmus liegt somit in der Größe der beiden gewählten Primzahlen p und q, da es – bei entsprechender Größe von p und q – nahezu unmöglich ist, nur durch Kenntnis der öffentlichen Schlüssels n und e den geheimen Schlüssen d zu eruieren. Noch 1993 schätzte man, dass die Faktorisierung einer 130-stelligen Zahl n in ihre zwei Primzahlen Millionen von Jahren benötigen würden. Tatsächlich gelang dies durch ständige Verbesserungen der Rechnerleistung ein Jahr später (vgl. Mekelburg 2004). Heute werden unwahrscheinlich große Werte für p und q genutzt, so dass das RSA-Verfahren auf lange Sicht hin wohl das sicherste asymmetrische Verfahren bleiben wird (vgl. Emmel). Eine generelle Sicherheit wird und kann es jedoch nie geben.


Onlinequellen:

Cisco Systems: RSA. In: http://www.ffpress.net/Kunde/CIS/GL/ (10.11.2005)

Emmel, S.: RSA-Verfahren als Meilenstein der Kryptologie. In: http://mnd-w1.fh-friedberg.de/25Jahre/beitraege/rsa.html (10.11.2005)

Grupp, Andreas (2001): Verschlüsselung mit "Pretty Good Privacy". In: http://www.elektronikschule.de/~grupp/pgp/intro.html (10.11.2005)

Mekelburg, Hans-G. (2004): Verschlüsselte Botschaften. Moderne asymmetrische Verfahren. In: http://home.nordwest.net/hgm/krypto/mod-asym.htm (10.11.2005)