Digitale Verschlüsselung

Der Austausch eines gemeinsamen, geheimen Schlüssesls zwischen Sender und Empfänger, ohne dass es eine dritte, unbeteiligte Person mitbekommt, stellt meist ein Problem dar. Martin Hellman, Whitfield Diffie und Ralph Merkle versuchten dieses Problem zu lösen und haben dazu den Diffie-Hellmann-Algorithmus entwickelt. Dieser ermöglicht den Austausch eines geheimen Schlüssels über eine unsichere Verbindung [Hilbig, 2015].

Wie funktioniert dieser Algorithmus?

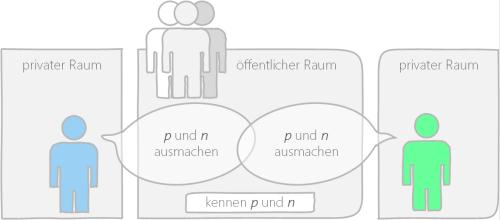
Damit sowohl Sender als auch Empfänger einen gemeinsamen, geheimen Schlüssel erstellen können, müssen sie eine Primzahl p und eine natürliche Zahl n vereinbaren. Wichtig dabei ist, dass die natürliche Zahl n kleiner als die Primzahl p sein muss! Diese Vereinbarung können sie ohne weiteres im öffentlichen Raum treffen [Hilbig, 2015].

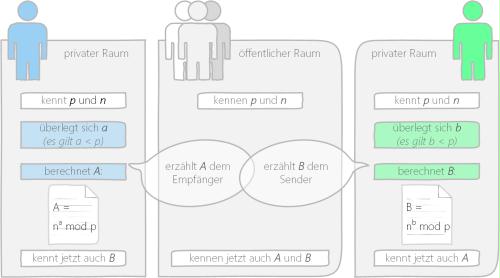
Nun wählt der Sender eine geheime, nur für ihn bestimmte Zahl a, die kleiner als p ist. Der Empfänger wählt ebenfalls eine geheime, nur für ihn bestimmte Zahl b, die kleiner als p ist. Der Sender berechnet anhand von a mittels Algorithmus nun A und der Empfänger anhand von b mittels Algorithmus B. Wie der Algorithmus lautet, ist in der folgenen Abbildung angeführt. Anschließend tauschen Sender und Empfänger A und B im öffentlichen Raum aus [Hilbig, 2015].

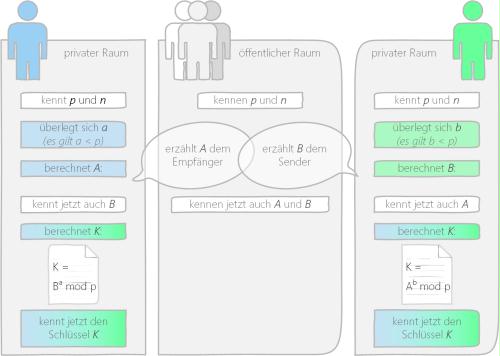
Nachdem Sender und Empfänger A und B ausgetauscht haben, können beide den Schlüssel K berechnen. Die Personen im öffentlichen Raum kennen jedoch nur p, n, A und B - zur Berechnung des Schlüssels K benötigen sie jedoch auch a und b. Daher ist es ihnen nicht möglich, den Schlüssel K zu berechnen [Hilbig, 2015].

Quelle:

[Hilbig, 2015] Hilbig, André; Diffie-Hellman-Algorithmus - Schlüsselaustausch. http://ddi.uni-wuppertal.de/material/spioncamp/dl/austausch-diffie-hellman-station2.pdf; Zugriff am 20.03.2015.