Die Ausarbeitung sind als .pdf auch unter Wavelets_JP2 (pdf, 867 KB) und den Vortrag unter Wavelets (pdf, 447 KB) zu finden.

Inhalt:

1. Die Notwendigkeit von Kompression 4

2. Wavelets und JPEG2000 4

2.1. Datenreduktion und die menschliche Physiologie 4

2.2. Ein kurzer Rückblick: JPEG-Kompression 5

2.3. Wavelets 5

2.4. Wavelets innerhalb JPEG2000 6

2.5. JPEG2000 8

2.6. Die fraktale Kompression 9

3. Die Wahl des geeigneten Komprimierungsverfahrens 10

4. Quellenverzeichnis: 11



1. Die Notwendigkeit von Kompression

In den letzten Jahren hat die Qualität der digital gespeicherten Daten wie Bild, Ton und Video durch bessere Auflösungen rapide zugenommen. Das damit eng zusammenhängende anfallende Datenvolumen verlangt nach immer stärkeren Kompressionsverfahren, die die derzeit gängigen Verfahren wie z.B. JPEG zur Bildkompression ablösen sollen. Diese Forderung hat vor allem mit dem ständig steigenden Datentransfer auch von großen Bild-, Ton- und Videodateien per Internet Bestand.
Wurden Ende der 80er Jahre noch Bilddateien hauptsächlich in dem vom US-Onlinedienst CompuServe 1987 eingeführten Graphic Interchange Fomat (GIF) übermittelt, setzte sich Anfang der 90er immer mehr der von der Joint Photographic Experts Group 1988 verabschiedete Standard JPEG zur Kompression von Bildern durch. Hauptgrund lag hier in der geringen Farbtiefe von GIF-Dateien. Das mit 16.7 Mio. Farben arbeitende JPEG dagegen überträgt reale Echtfarbbilder in für das Internet geeignete Größen bei minimalem Qualitätsverlust und einem Kompressionsfaktor von 10 bis 20.
Jedoch bietet JPEG bei Kompressionsraten von 1:30 und höher keine geeignete Qualität mehr und es werden Moiré- und Blockmuster innerhalb des Bildes sichtbar. Dies ist vor allem ein Problem bei sehr großen zu übertragenen Daten, bei denen starke Kompressionsfaktoren gefragt sind. Hier findet der seit 1997 von einer weiteren Gruppe der JPEG-Organisation entwickelte und im Januar 2001 von der ISO verabschiedete JPEG 2000-Standard Einsatz, der Kompressionsraten von bis 1:65 ohne gravierende Qualitätsverluste zulässt.
Doch was geschieht bei den einzelnen Verfahren und wo genau liegen die Unterschiede?

Die größten Unterschiede liegen in der Art der Transformation der Bild- oder Audiodaten von dem Orts- oder Zeitraum in den Frequenzraum. Hier kommt je nach Verfahren und Art der Daten die DCT (engl. Discrete Cosinus Transform = Diskrete Kosinus-Transformation), die FFT (engl. Fast Fourier Transform = Schnelle Fourier-Transformation) oder die FWT (engl. Fast Wavelet Transform = Schnelle Wavelet-Transformation) zum Einsatz.
Nach der Transformation der Daten, die eine bessere Auffindung der redundanten Daten durch eine veränderte Darstellung zum Ziel hat, finden eine Quantisierung sowie eine Kodierung statt, wobei nur die Quantisierung die Datenverluste nach sich zieht. Diese beiden Schritte unterscheiden sich nur wenig bei den einzelnen Verfahren.
Im Folgenden soll auf die Verfahren der Bildkompression, vor allem der JPEG 2000-Kompression sowie der darin enthaltenen Wavelet-Transformation eingegangen und Unterschiede zum älteren JPEG-Standard sowie Vor- und Nachteile der einzelnen Verfahren aufgezeigt werden.

2. Wavelets und JPEG 2000
2.1. Datenreduktion und die menschliche Physiologie
Alle Verfahren zur Datenreduktion können in verlustfreie und verlustbehaftete Reduktion eingeteilt werden. Eine Ausnahme stellt hier die JPEG 2000-Kompression dar, da hier wahlweise verlustfrei oder verlustbehaftet komprimiert werden kann.
Die verlustfreie oder auch Redundanzreduktion arbeitet mit einer Kodierung der in der Datei enthaltenen Zeichen (bezeichnet als Alphabet) oder Zeichenfolgen durch beispielsweise eine Baumdarstellung, wie sie bei der Huffman-Kodierung ihren Einsatz findet. Diese Technik wird z.B. bei der Kompression von Textdokumenten eingesetzt, da hier eine verlustbehaftete Reduktion schwerwiegende Fehler in der Speicherung des Textes nach sich ziehen würde.
Bei der verlustbehafteten Datenreduktion oder Irrelevanzreduktion dagegen werden die menschlichen Wahrnehmungseigenschaften bei der Speicherung von Informationen

berücksichtigt. So ist beispielsweise das menschliche Auge nicht in der Lage, starke und häufige Farbwechsel wahrzunehmen, reagiert jedoch stark auf Helligkeitsunterschiede.
Diese Tatsache wird nun bei der Datenreduktion ausgenutzt, indem das Bild einem Tiefpassfilter zur Farbreduktion unterworfen wird und nach der Frequenzanalyse die hohen Frequenzen, d.h., die schnellen Farbwechsel eines Bildes, verworfen bzw. auf niedrigere Frequenzen quantisiert werden.

2.2. Ein kurzer Rückblick: JPEG-Kompression

Das Verfahren der JPEG-Kompression, das de fakto kein Dateiformat, sondern ein Standard zur Kompression von Bilddateien ist, arbeitet mit der DCT zur Transformation der Bilddaten vom Orts- in den Frequenzraum. Vor der Transformation wird das Bild nach JPEG Standard in 8x8 große Pixelblöcke unterteilt. Dies verhindert Moiré-Effekte und mindert den Rechenaufwand, der bei der DCT überproportional (n•log(n)) ist. Eine globale Berechnung des Bildes hätte weiterhin eine Verfälschung der Koeffizienten der niedrigeren Frequenzen durch Koeffizienten höherer Frequenzanteile zur Folge und würde die Speicherung des gesamten Bildes negativ beeinflussen.
Die DCT arbeitet mit einem Satz an reellen Kosinusfunktionen zur Darstellung der Farbwerte durch Frequenzen innerhalb eines solchen 8x8 Blockes. Das Ergebnis der DCT ist wiederum eine 8x8 Matrix und hat noch keine Datenverluste zur Folge. Der erste Koeffizient (an der Stelle (0,0)) gibt die Gewichtung der niedrigsten Frequenz im Frequenzspektrum wieder und gilt als Durchschnittswert. Vertikal und Horizontal nimmt die Frequenz, die durch die Koeffizienten der Matrix gewichtet werden, zu. Die Werte der Koeffizienten nehmen dabei rapide ab, was einer geringen Repräsentation von hohen Frequenzen und somit einer Informationsverdichtung in den ersten Koeffizienten entspricht.
Diese Tatsache kann bei der anschließenden Quantisierung der Matrix zur Kompression ausgenutzt werden. Hierbei findet der eigentliche Informationsverlust statt, da die Werte der Koeffizienten innerhalb der 8x8 Matrix auf einige wenige Durchschnittswerte gebracht , also gerundet werden.
Nach der Quantisierung findet eine Lauflängenkodierung (RLE = Run Length Encoding, engl.) und darauffolgend eine Entropiekodierung, die Huffman-Kodierung, statt.

2.3. Wavelets

Näher betrachtet unterscheiden sich die Arten der Transformationen, sei es nun die DCT, die FFT oder die FWT, die bei den einzelnen Reduktionsverfahren Einsatz finden, wenig voneinander - die Art der Basisfunktionen sind viel entscheidender.
Wirken bei der DCT ein bestimmter Satz von kontinuierlichen reellen Kosinusfunktionen, so arbeitet die FFT mit kontinuierlichen komplexen Sinusoiden und die FWT mit Wavelets.
Wavelets sind kleine nach außen hin auslaufende (kleiner werdende) Wellenfunktionen (Wellchen = Ondoloette = Wavelet), deren Integral, d.h, deren Fläche unter der Funktion gleich 0 ist. Das einfachste und auch bekannteste dieser Wavelets ist das Haar-Wavelet, welches die Abbildung unten zeigt.








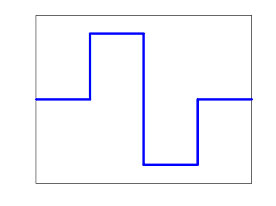
(1) Daubechies 2 Wavelet (Haar-Wavelet)

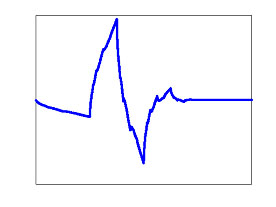
(2) Daubechies 4 Wavelet


Der Vorteil dieser Wavelets liegt in der zeitlichen und örtlichen Begrenzung der Funktion. Während bei der JPEG-Kompression das Bild in 8x8 Pixelblöcke unterteilt werden muss, um die Auswirkungen höherer Frequenzanteile auf niedrigere Frequenzen einzugrenzen, da die JPEG-Koeffizienten den Bildinhalt global beschreiben, wäre eine Transformation des kompletten Bildes mit der Wavelet-Transformation unproblematisch, da die Wavelets lokal wirken und mittels Skalierung und Translation an den jeweiligen Frequenzbereich (z.B. Bildbereich) flexibel angepasst werden können.

2.4. Wavelets innerhalb JPEG2000

Der Algorithmus der Wavelet-Transformation ist mit linearem Aufwand ( = n) implementiert und arbeitet rekursiv, was aus Abbildung (4) und (6) deutlich hervorgeht.


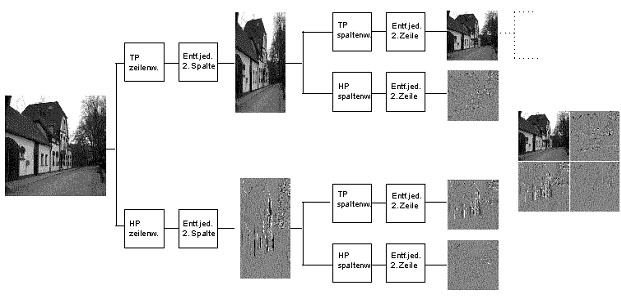
(3) 1. Iteration, Schema des Bildes nach horizontaler & vertikaler Tief- und Hochpassfilterung







(4) Ausgangsbild (5) Gefilterte Teilbilder nach 2. Iteration

Jeder Durchlauf erzeugt eine kleinere geglättete Darstellung des Originalbildes (das Ergebnis der doppelten Tiefpassfilterung) und 3 komplementäre Bilder, die die hohen Frequenzen enthalten. Zu Anfang der Berechnung wird das gesamte Bild simultan einer Tief- und Hochpassfilterung in Zeilenrichtung (x-Richtung) unterzogen (Bild (3)). Daraufhin können, da jetzt nur noch genau die Hälfte der Geamtinformation pro Darstellung vorhanden ist, die Hälfte der Spalten aus jedem Bild entfernt werden. Anschließend wird dieselbe Filterung in Spaltenrichtung (y-Richtung) durchgeführt und pro Ergebnisdarstellung wiederum die Hälfte der Zeilen entfernt.
Die einzelnen Teilbilder werden danach gespeichert und stellen folgende Informationen für das Gesamtbild zur Verfügung:
- LL ist die geglättete und verkleinerte Darstellung des Originalbildes. Dies kann mit einem Bild mit verringerter Auflösung gleichgestellt werden.
- LH repräsentiert vor allem die horizontale Bildelemente
- In HL sind besonders die vertikalen Bildstrukturen wiederzufinden
- HH gibt durch doppelte Hochpassfilterung vor allem die diagonalen Strukturen des Bildes wieder

Die oben genannten Feststellungen lassen sich anhand der Abbildung (5) visuell sehr gut nachprüfen.
Dieser Algorithmus kann immer wieder auf das verkleinerte tiefpassgefilterte Bild angewendet werden (Rekursion), bis dieses nur noch 1 Pixel groß ist. Wohlgemerkt gehen dabei keinerlei Informationen verloren, das Bild wird nur immer wieder in seine hoch- und niederfrequenten Anteile zerlegt.
Die dafür benötigte spezielle Wavelet-Funktion wird bei jeder weiteren Iteration um den Faktor 2 skaliert und filtert die Datenmenge bei jedem Filterschritt genau um die Hälfte. Diese Eigenschaften erfüllen nur sogenannte dyadische Wavelets, die der im Jahr 1989 durch Stéphane Mallat und Yves Meyer mit Hilfe der Muliskalenanalyse (Multi Resolution Analysis = MRA, engl.) entwickelten Schnellen Wavelet-Transformation zugrunde liegen und rekursiv aufgebaut sind.
Die Theorie der Multiskalenanalyse geht davon aus, dass das visuelle System des Menschen Bilder in verschiedenen Auflösungen (Multi Resolution) wahrnimmt. Dies findet bei der Schnellen Wavelet-Transformation innerhalb JPEG 2000 Anwendung.


2.5. JPEG 2000

Nach erfolgter Transformation der Bilddaten wird wie gewohnt eine Quantisierung der resultierenden Koeffizienten durchgeführt, bei der die Datenverluste entstehen. Anschließend werden die Daten einer Lauflängenkodierung und einer Entropiekodierung unterzogen. Dabei findet jedoch nicht die Huffman-Kodierung sondern die effizientere Arithmetische Kodierung, die mit Intervallen arbeitet und sehr nah an die Entropieschranke reicht ihren Einsatz.
Viele der Vorteile des JPEG 2000-Formats liegen bereits durch nähere Betrachtung des Wavelet-Transformation auf der Hand:
• Höhere Kompressionsraten bei besserer Qualität gegenüber Formaten wie JPEG
• Progressiver Bildaufbau mit Levels of Detail, da die Anordnung der komprimierten Daten einen gezielten Zugriff auf verschiedene Auflösungs- und Qualitätsstufen ermöglicht, ohne erst das gesamte Bild zu dekomprimieren
• Weniger Rechenaufwand gegenüber JPEG, da der Aufwand der Wavelet-Transformation linear ist
• Keine Blockmusterbildung, da Verluste im Bereich der Schärfe entstehen, nicht im Farbverlauf
• Größere Robustheit gegenüber Übertragungsfehlern, die sich gegenüber JPEG nur lokal auswirken

Darüber hinaus gibt es noch teilweise durch den Standard JPEG 2000 festgelegte Vorteile:
• Ähnlich dem PNG-Format besitzt JPEG 2000 bis zu 16 bit Tiefe pro Farbkanal. Dies bedeutet eine Unterstützung von bis zu 65536 Graustufen oder 281 Billionen Farben.
• Möglichkeit der ROI (Region of Interest)-angepassten Komprimierung, d.h., durch Anpassung der Filterung der Wavelets mittels Skalierung kann die Stärke der Kompression an interessanteren Regionen gegenüber weniger interessanten Regionen des Bildes vorgenommen werden
• Übergroße Bilder mit mehr als 65536 x 65536 Pixeln können komprimiert werden (JPEG war bis zu dieser Größe limitiert)
• Stufenloser Übergang von verlustfreier zu verlustbehafteter Kompression
• Zusatzkanäle z.B. für Transparenzeigenschaften vorhanden
• Speicherung von Metadaten im XML-Format zur Bildbeschreibung und für Copyright-Informationen
• JPEG 2000 bietet bis zu 256 Farbkanäle und ist damit in der Lage, RGB- und CMYK-Daten gleichzeitig zu speichern

JPEG 2000 ist hiermit nicht einfach nur eine Erweiterung des JPEG-Standards, es ist ein völlig neues Format, das zwar die Vorteile von JPEG aufweist, sie jedoch noch bei weitem übertrifft.
Leider gibt es auch bei JPEG 2000 einige Nachteile, die aber vor allem in der Verbreitung des Formats und Anwendung zu finden sind. So wird das Format mit der Dateiendung .jp2 von vielen Bildbearbeitungswerkzeugen wie auch von den gängigen Browsern noch nicht unterstützt – es muss ein geeignetes PlugIn installiert werden. Auch ist das Format bisher kaum im Internet zu finden.
Bei Kompressionsraten über 60 – 70 wird auch die Qualität der mit JPEG 2000 komprimierten Bilder stark beeinträchtigt. Hierfür würde dann die sehr rechenintensive fraktale Kompression in Frage kommen.
2.6. Die fraktale Kompression

Auf das Verfahren der fraktalen Kompression soll hier nur kurz eingegangen werden. Mehr dazu ist in den Quellen und Literaturhinweisen weiter unten zu finden.
Ziel der fraktalen Kompression von Bildern ist es, das Gesamtbild durch eine iterierte Funktion zu beschreiben, wobei die Tatsache ausgenutzt wird, dass in jedem Bild Selbstähnlichkeiten auftreten. Probleme treten bei der Auffindung so einer Funktion auf. Das Bild muss nach Selbstähnlichkeiten durchsucht werden, d.h., es müssen Teilbilder gefunden werden, die anderen Teilen des Bildes mit oder ohne Skalierung, Translation und anderen affinen Transformationen ähnlich sind. Dazu wird das Ausgangsbild partitioniert, wobei es unterschiedliche Verfahren zur Partitionierung gibt, die im Folgenden aufgeführt und abgebildet sind:


(6) a) & b)


(7) c) & d)

a) zeigt die Unterteilung des Bildes in Quadrate fester Größe (einfachste Möglichkeit)
b) Quadtree: die Unterteilung erfolgt je nach Inhalt in kleinere oder größere Quadrate
c) HV: Die Unterteilung in Rechtecke wird immer an einer vom Bildinhalt abhängigen Stelle in 2 Rechtecke unterteilt
d) Triangular: im Prinzip wie HV, nur wird hier mit Dreiecken gearbeitet, die jeweils in 4 kleinere Dreiecke unterteilt werden
Die Teilbilder werden daraufhin nach Ähnlichkeiten untersucht. Dieser Prozess ist extrem rechnintensiv während die Dekompression sehr schnell und mit wenig Aufwand funktioniert, da hier das Bild einfach durch die Iteration der Funktion aufgebaut wird. Somit handelt es sich bei der fraktalen Kompression um ein unsymmetrisches Verfahren.

3. Die Wahl des geeigneten Komprimierungsverfahrens

Folgend ist ein Vergleich von JPEG, Wavelet und der Fraktalen Kompression mit zwei unterschiedlichen Partitionierungstechniken abgebildet. Hier wurde ein Grauwertbild mit 512 x 512 Pixeln als Quelle genommen. Die Qualität der Ergebnisse wurde mit dem PSNR (Signalrauschabstand) gemessen. Weiter unten finden sich Beispielbilder für JPEG und JPEG 2000 mit verschiedenen Kompressionsraten.

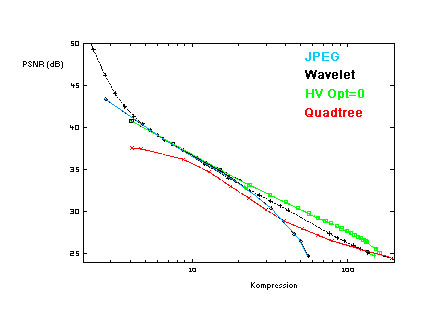
(8) Vergleich von JPEG, JPEG 2000 und fraktaler Kompression


(9) Original (links), JPEG 1:19 (mitte), JPEG 2000 1:50 (rechts), JPEG 2000 1:100 & 1:200 (unten)

Abschließend ist zu sagen, dass bei Kompressionsraten von 1:5 bis 1:25 alle Verfahren gleich gut arbeiten, wobei dem JPEG-Verfahren hier der Vorzug zu geben ist, da es am weitesten verbreitet ist. Bei niedrigen Raten von bis zu 1:5 liefert die Wavelet-Kompression die beste Qualität. Raten von über 1:25 behandelt die fraktale Kompression mit der HV-Partitionierung mit den wenigsten Verlusten und somit Störungen.
Wavelet- und fraktale Kompression sind somit nahezu in ihrer Qualität vergleichbar. Die fraktale Kompression schlägt mit einer hohen Rechendauer von einigen Minuten bei der Kompression jedoch sehr negativ zu Buche. Vorteile sind hier die schnelle Berechnung des Bildes bei der Dekomprimierung und die theoretisch unendliche Vergrößerungsmöglichkeit, da Details immer wieder neu verfeinert werden können, obwohl eine reale Darstellung des Bildes ab einem gewissen Grad natürlich begrenzt ist.
Wie in den Abbildungen unter (9) für jeden ersichtlich ist, liefert JPEG 2000 bei dem 2,5- fachen der Kompressionsrate sogar visuell immer noch bessere Ergebnisse, da die Qualitätseinbußen im Bereich der Unschärfe liegen, die das menschliche Auge nicht so stark wahrnimmt wie die Blockmusterbildung des JPEG-Verfahrens.
Da viele Geräte wie z.B. Digitalkameras noch nicht in der Lage sind, Verfahren wie die Wavelet- oder die fraktale Kompression zu implementieren, die Verbreitung der Formate noch sehr gering ist und auch die Notwendigkeit solch starker Kompressionsverfahren im privaten Sektor nicht unbedingt gegeben ist, fällt die Wahl wohl auch weiterhin auf JPEG. Nur für professionelle Einsatzgebiete wie Bilddatenbanken, wissenschaftliche, medizinische oder militärische Anwendungen ist das JPEG 2000-Verfahren mit Eigenschaften wie die hohe Kompressionsrate bei guter Qualität, linearem Rechenaufwand und den integrierten Metadaten sinnvoll.

4. Quellenverzeichnis:
Wavelet & JPEG2000:

[1] „Bilder schrumpfen“ von Manfred Bertuch: http://www.heise.de/ix/artikel/2001/08/108/
[2] „Wavelet-Tutorial“ von Prof. Dr.-Ing. R. Urbansky des Instituts für Nachrichtentechnik der TU Kaiserslautern: http://nt.eit.uni-kl.de/wavelet/index.html
[3] „Wavelet-Kompression“ von Rainer Steinwandt, publiziert beim Institut für Betriebs- und Dialogsysteme der Universität Karlsruhe: http://i31www.ira.uka.de/docs/semin94/03_Wavelet/
[4] Beschreibung des Wavelet-Verfahrens der FH Jena:
http://www.fh-jena.de/contrib/fb/et/personal/ansorg/ftp/wavelet/wavelet.htm
[5] „Wavelet-Kompression“ von Jörg Cassens an der Universität Oldenburg: http://condor.informatik.uni-oldenburg.de/lehre/WS01-SigBildVer/wavelet02.pdf
[6] Wikipedia – Die freie Enzyklopädie:
http://de.wikipedia.org/wiki/Wavelet
http://de.wikipedia.org/wiki/Wavelet-Transformation
http://de.wikipedia.org/wiki/JPEG2000
[7] Offizielle JPEG2000-Seite: http://www.jpeg.org

JPEG, sowie Geschichtliches:
[8] „Bildformate“ von div. Autoren:
http://www.scheib.info/downloads/Projekt_Bildformate.pdf

Fraktale:
[9] „Fraktale Kompression“ von Jochen Quante, publiziert beim Institut für Betriebs- und Dialogsysteme der Universität Karlsruhe: http://i31www.ira.uka.de/docs/semin94/04_Fraktal/
[10] Wikipedia – Die freie Enzyklopädie: http://de.wikipedia.org/wiki/Fraktale_Kompression

Sonstige Informationen zu Datenkompression, Kodierungsalgorithmen usw.:
[11] Wikipedia – Die freie Enzyklopädie: http://wikipedia.de

Bildquellen:
(1), (2), (4), (5): •http://nt.eit.uni-kl.de/wavelet/index.html
(3), (9): http://www.fh-jena.de/contrib/fb/et/personal/ansorg/ftp/wavelet/wavelet.htm
(6), (7), (8): http://i31www.ira.uka.de/docs/semin94/04_Fraktal/





© by Björn Hoffmann – FHTW Berlin bjoern.hoffmann@fhtw-berlin.de

...maaaaaaan!

RICHTIIIIIIIIIIIIIIIIIIIIIIIIIIIICCCCCCCCCCCH

Tja, modernste Weltraumtechnik macht es möglich...